
In the Spring of 2007 I took a course called “Paul Revere: Tough as Nails” (Materials Science course plus History of Technology course), and the final project my team and I chose was to design lesson plans for teaching non-Newtonian fluid dynamics and significance to elementary, high school, and college students. This post outlines the lesson plan ideas for a college audience. To see the main project overview go here.
Analyzing Non-Newtonian Fluids
One of the most interesting things about non-Newtonian fluids is that scientists don’t really understand how they work. There are many proposals and models for their behavior, but no direct and tested answers. To truly understand non-Newtonian fluids, scientists must contrast their behavior with Newtonian fluids, using multiple qualitative and quantitative tests.
Impact Testing
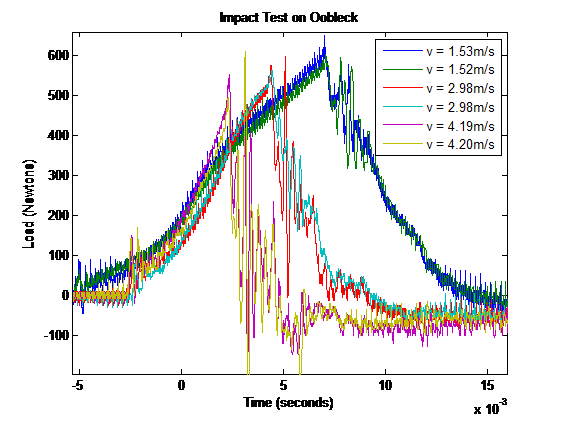
Oobleck, a cornstarch-based sheer-thickening fluid, is an excellent specimen upon which to conduct these experiments. One of the simplest and easiest to quantify is an impact test. One would generally predict that the faster the impact, the more likely the oobleck is to shatter. The slower the impact, the more liquid-like it will remain, slowly absorbing the force. One series of tests on oobleck is shown below.
As these data clearly demonstrate, the oobleck reacts exactly as hypothesized. Compare the integrals of the force over time of each impact. Slower impacts allow the oobleck to absorb more energy as it remains in a more liquid state. Faster impacts cause the oobleck to become much harder, absorbing less energy in a more elastic collision. This behavior is evident in the irregular spikes in the faster data, while the more liquid oobleck generates a smooth force curve.
Taking the integral of the curves using the cumulative summation method in MATLAB, we found that the integral of the 1.5 m/s drop was 4.8465Ns, the 3 m/s drop was 1.2927Ns, and the 4.2 m/s drop was 0.1091Ns. It is apparent that these values are not linear.
Microstructure
However, all this analysis is useless if it cannot be applied directly to the microscopic structure of the water and cornstarch itself. Scientists do not currently understand why non-Newtonian behavior exists, but by observing the qualities of the substrates, it is possible to understand how to vary the material’s properties. One study discovered that as particle size increases, dilatant behavior became more obvious. This was limited as the grains of cornstarch burst, returning the liquid at high concentrations to less interesting behavior[[1]](file:///C:/Users/Marcotuts/Documents/Classes/2nd%20Semester/MatSci/Project%203/All%20Together%20Now.docx#_ftn1).
Applications
Scientists are currently exploring Non-Newtonian fluids for a variety of uses. Many of these are hypothetical and yet to be realized, while others have been studied more extensively.
Propulsion
The common slug utilizes a non-Newtonian mucus to propel themselves across a surface. The mucus acts as an interface between the shear force of their muscles and the surface. On portions of the slug that are still, the fluid thickens and holds the slug in place. Where the slug is moving, the mucus thins and allows the slug to extend. This motion is one possible model for small, efficient wall-climbing robots. Slug-like robots are not a new idea, but by understanding the nature of the mucus interface, scientists have discovered ways to make this motion most effective. The usefulness of a given robot is highly dependent on their synthetic mucus. An MIT study found that the ideal synthetic slug mucus must minimize post-yield viscosity, while yield-stress of the slime depends on the robot.[[2]](file:///C:/Users/Marcotuts/Documents/Classes/2nd%20Semester/MatSci/Project%203/All%20Together%20Now.docx#_ftn2)
Artificial Silk
Synthetic spider’s silk has been a holy grail of materials and polymer science for decades. Spider’s silk is roughly as strong as steel, yet one fifth as dense[[3]](file:///C:/Users/Marcotuts/Documents/Classes/2nd%20Semester/MatSci/Project%203/All%20Together%20Now.docx#_ftn3). While fibers such as Kevlar are comparable to spider’s silk’s properties, spider’s silk is made from simple sources, without hazardous industrial chemicals. To make silk, the spider first produces a protein gel. She then extrudes it through a series of organs, with the silk finally exiting her spinneret and drying. The final strand has a complex, tightly woven structure.
Recent studies have shown that the protein gel exhibits Non-Newtonian properties[[4]](file:///C:/Users/Marcotuts/Documents/Classes/2nd%20Semester/MatSci/Project%203/All%20Together%20Now.docx#_ftn4). Scientists hypothesize that by understanding the non-Newtonian behavior of the gel, they can finally duplicate the exact processes required to synthesize artificial silk. One recent study discovered that the gel is a shear-thinning liquid, which has many important implications in silk synthesis[[5]](file:///C:/Users/Marcotuts/Documents/Classes/2nd%20Semester/MatSci/Project%203/All%20Together%20Now.docx#_ftn5). Because the actual extrusion process has extremely important effects on the final characteristics of the silk, understand the gel’s precise behavior is vital. Hypothetically, scientists could use this knowledge to create silks with specific properties, possibly even superior to natural silks. This could offer safer, organic plastics that are more environmentally sound than the petroleum-based polymers of today.
Biomedical Uses
Many natural biological substances exhibit non-Newtonian behavior. Understanding and controlling these behaviors are important, specifically in the fields of drug-delivery and wound healing[[6]](file:///C:/Users/Marcotuts/Documents/Classes/2nd%20Semester/MatSci/Project%203/All%20Together%20Now.docx#_ftn6). Bones are one such example of a non-Newtonian substance – they can sustain greater forces at higher loading rates, but subsequently become more brittle. In understanding this behavior, scientists can create prosthetics that more closely mimic the strength of real limbs[[7]](file:///C:/Users/Marcotuts/Documents/Classes/2nd%20Semester/MatSci/Project%203/All%20Together%20Now.docx#_ftn7). Bones are remarkably efficient structures, and mimicking their strengths could produce better building materials.
Joints are another excellent example of biological non-Newtonian fluids. Synovial joints – such as the joints in the wrist – have 1/3 less friction than an object on ice. They are remarkably efficient for the loads they bear. This is largely due to the shear-thinning lubricants between bone surfaces. This behavior could be exploited to create more efficient mechanical bearings, as well as better artificial joints or limbs. Other possible biomedical uses of non-Newtonian fluids include artificial tendons, extremely thin sutures for delicate surgery, and “smarter” wound coverings.
Safety
Shear-thickening fluids have many possible uses in dampening impacts. One group of researchers has impregnated Kevlar armor with a shear-thickening nano-fluid[[8]](file:///C:/Users/Marcotuts/Documents/Classes/2nd%20Semester/MatSci/Project%203/All%20Together%20Now.docx#_ftn8). This hardens the fabric when stabbed or shot – allowing it to be flexible and comfortable in everyday use and strong when needed. Many other safety devices could benefit from non-Newtonian behavior. Consider an airbag, which inflates through a rapid explosion into a fabric bag. While better than hitting the dashboard, airbags inflate with such force as to sometimes break bones, cause burns, or otherwise harm the driver. Utilizing a non-Newtonian fluid would allow a safety device to react better to the driver, dampening his or her impact with a force proportional to the strength of the accident.
[1] http://www.blackwell-synergy.com/doi/abs/10.1111/j.1745-4603.1995.tb00800.x
[2] web.mit.edu/ewoldt/www/pubs/Ewoldt_ACS_2007_PMSE-387.pdf
[3] http://en.wikipedia.org/wiki/Spider_silk
[4] http://web.mit.edu/newsoffice/2006/spider.html
[5] www.pmmh.espci.fr/~jbico/kojic06.pdf
[7] http://www.orthobiomech.info/biomechanics.htm
[8] http://www.sciencentral.com/articles/view.php3?type=article&article_id=218392807